Snow in JavaScript

May 17, 2010∙6 min read

Winter is finally over, but we can still make nice digital snow to cool us down during hot summer days. We will start by considering the path snow flakes take before they hit the ground, then we will find out how to implement it using mathematics. Finally we will implement this idea using Object Oriented Programming in JavaScript.

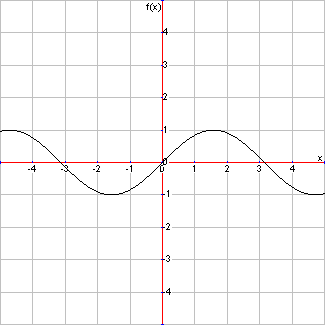
If you think of the fall pattern of snow in terms of a math function, you will realize it is in fact a sin function (see figure 1). Now all we have to do is to express x as a function of y. We will change y using a linear function (i.e increase y by a constant value) and calculate x based on that. So x = sin(y), y = t * c where t is time and c is a constant value.

Figure 1 - Sin graph resembles the path snow flakes take when falling down. Imaging the graph on its side may help you visualize how this works.

Note that it is easy to express both x and y as a function of t as well. This can be quite useful when we want to make our animation dependent on time alone. Say we wanted the animation to last exactly 5 seconds, we could then limit the range of the t variable to help us do that. In our case, we won't need that, it will be simpler to stick to our original formulas.

Next we need to use transformations to help us bend the sin graph to our needs. If you look at figure 1, you will notice the f(x) only varies from -1 to 1, but that means that in our formula x will only be moving across 3 pixels (-1, 0 and 1) since we use integers for pixels. Instead, we want our x to vary between -W and W where W is some constant width. To do this we change our x to be x = W * sin(y) this is known as changing the amplitude of the sin graph. So this transforms our graph to be in a desired amplitude range. But what about the wavelength, well it is exactly 2π which we want to change to be an arbitrary value L. Let us change the equation for x again to be: x = W * sin((2π / L) * y). The transformations we just performed are based on this formula:

y = a + b sin(k(x - c))

The period length is 2π / k. Amplitude is b. Shifting the graph up or down is achieved by using a. Which we will later use to position our snow particles. Shifting the graph left or right is achieved by usingc. But we will not need it here.

If you plug in the changes we made to the original sin graph, you will see that we indeed get the results we want. An online graphing calculator is also a good way to play with graphs to create even more interesting animations. A simple online sin graph transformation can be used or a more generic graphing calculator can be used to find more interesting curves.

var MAX_SPEED = 5;
var MIN_SPEED = 10;

var MAX_PATH_WIDTH = 20;
var MIN_PATH_WIDTH = 50;

var MAX_PATH_HEIGHT = getDocumentHeight();
var MIN_PATH_HEIGHT = 100;
var NUM_OBJECTS = 50;

var MAX_SIZE = 32;
var MIN_SIZE = 20;

var snow = [];

/**
 * This function is a cross-browser function that gets the document height.
 * @return Document height if able to find it, otherwise -1.
 * @see http://www.howtocreate.co.uk/tutorials/javascript/browserwindow
 */
function getDocumentHeight()
{
  if(typeof(window.innerWidth) == 'number')
  {
    //Non-IE
    return window.innerHeight;
  }
  else if(document.documentElement && (document.documentElement.clientWidth || document.documentElement.clientHeight))
  {
    //IE 6+ in 'standards compliant mode'
    return document.documentElement.clientHeight;
  }
  else if( document.body && (document.body.clientWidth || document.body.clientHeight) )
  {
    //IE 4 compatible
    return document.body.clientHeight;
  }
  else
  {
    // Unable to find height
    return -1;
  }
}

/**
 * This function is a cross-browser function that gets the document width.
 * @return Document width if able to find it, otherwise -1.
 * @see http://www.howtocreate.co.uk/tutorials/javascript/browserwindow
 */
function getDocumentWidth()
{
  if(typeof(window.innerWidth) == 'number')
  {
    //Non-IE
    return window.innerWidth;
  }
  else if(document.documentElement && (document.documentElement.clientWidth || document.documentElement.clientHeight))
  {
    //IE 6+ in 'standards compliant mode'
    return document.documentElement.clientWidth;
  }
  else if( document.body && ( document.body.clientWidth || document.body.clientHeight ) )
  {
    //IE 4 compatible
    return document.body.clientWidth;
  }
  else
  {
    // Unable to find wodth
    return -1;
  }
}

/**
 * Returns a random number between min and max.
 * @param number min The lower bound of the range.
 * @param number max The upper bound of the range.
 * @return number A random number between min and max.
 */
function random(min, max)
{
  return Math.random() * (max - min) + min;
}

function sinGraph(value, height, waveLength)
{
  return height * Math.sin((2 * Math.PI / waveLength) * value);
}

/**
 * Create a new snow flake object in the specified starting position
 * @param Image imageObj The image object to be used as a snow flake
 */
function SnowFlake(imageObj)
{
  var that = this;

  this.imageObj = imageObj;
  this.interval = null;


  this._reset();
}

/**
 * Resets teh status of the object with new random values
 */
SnowFlake.prototype._reset = function() {
  var size;

  this.startX = random(0, getDocumentWidth());
  this.startY = -1 * random(0, getDocumentHeight());
  this.x = this.startX;
  this.y = this.startY;

  this.speed = random(MIN_SPEED, MAX_SPEED);
  this.pathWidth = random(MIN_PATH_WIDTH, MAX_PATH_WIDTH);
  this.pathHeight = random(MIN_PATH_HEIGHT, MAX_PATH_HEIGHT);

  size = random(MIN_SIZE, MAX_SIZE);
  this.imageObj.width = size;
  this.imageObj.height = size;
};

/**
 * Starts an infinite animation loop using the given function to move and change the size of the given object.
 */
SnowFlake.prototype._animation = function (funcMoveX, funcSizeWidth) {
  this.y += this.speed;

  if(this.pathWidth === 0 || this.pathHeight === 0)
  {
    this.x = funcMoveX(this.y) + this.startX;
  }
  else
  {
    this.x = funcMoveX(this.y, this.pathWidth, this.pathHeight) + this.startX;
  }

  // check if snow flake y value is out of the frame
  if(this.y >= window.innerHeight)
  {
    this._reset();
  }
  else
  {
    this.imageObj.style.top = parseInt(this.y, 10) + "px";
  }

  if(this.x <= window.innerWidth)
  {
    this.imageObj.style.left = parseInt(this.x, 10) + "px";
  }
};

/**
 * Starts the animation for this object. To stop the animation call stopAnimation.
 */
SnowFlake.prototype.startAnimation = function()
{
  var that = this;
  this.interval = setInterval(function(){ that._animation(sinGraph, null); }, 100);
};

/**
 * Stops the animation for this object. To start the animation again call startAnimation.
 */
SnowFlake.prototype.stopAnimation = function(){
  clearInterval(this.interval);
};


function initAnimation()
{
  var object;
  var newElementId;
  var html = "";
  var i;

  // add snow flakes images to the html
  for(i = 0; i < NUM_OBJECTS; i++)
  {
    newElementId = "snow" + i;
    html += "<img id=\"" + newElementId + "\"src=\"snowflake.png\" width=\"32\" height=\"32\" style=\"position: absolute;\" />";
  }

  document.body.innerHTML += html;

  // initialize the animation for the snow flakes
  for(i = 0; i < NUM_OBJECTS; i++)
  {
    object = document.getElementById("snow" + i);
    snow.push(new SnowFlake(object));
    snow[i].startAnimation();
  }
}

Here is the HTML code we use:

<html>
<head>
...
<style>
  body
  {
    overflow: hidden;
  }
</style>
</head>
<body onload="initAnimation();">
</body>
</html>

Note how flexable the code is, thanks to functional programming we can take any math function and plug it in as our movement pattern. This means that we are not limited to just snow, but we can in fact animating anything with the same code. For example if we wanted to animate falling leaves or falling rain just by changing the path function.

Another important thing to note is the use of random values to make the simulation (yes this is a simulation) more real. Since real life is more or less random, so is our animation. Randomness adds a great deal of realism and is used quite often throughout simulations.

Here is a demo page implementing this code. As you can see below, this makes a pretty neat effect :) (when used responsibly of course).

Update 1: Changed SnowFlake class to use prototype for methods instead of using this.MethodName. This reduced the memory footprint to about one fifth (7MB) of the original (35MB). Go prototypes! :)

Want to do this in HTML5 with no Javascript? Wordpress San Francisco had a great session about it. Check it out:

http://2011.sf.wordcamp.org/session/css3-features-making-snow-in-the-summer-without-javascript